Conditioning and Independence
Conditioning
Conditional probability is defined as \(\mathbb P(A\lvert B)=\frac{\mathbb P(A\cap B)}{\mathbb P(B)}\), assuming \(\mathbb P(B)>0\). Conditioning makes the events outside of \(B\) have zero probability. Also note \(A\subseteq B\implies\mathbb P(A\lvert B)=\frac{\mathbb P(A)}{\mathbb P(B)}\).
Conditional probabilities share properties of ordinary probabilities.
| Axiom | Formula |
|---|---|
| Non negativity | \(\mathbb P(A\lvert B)\geq 0\) |
| Normalization | \(\mathbb P(\Omega\lvert B)=1\) |
| (finite) Additivity | \(\begin{align}A_i\cap A_j=\emptyset, i\neq&j\implies\\\mathbb P(A_1\cup A_2\cup\dots A_n\vert B)&=\sum_{i=1}^n\mathbb P(A_i\lvert B)\end{align}\) |
Main three tools
Obtained from application of the definition \(\mathbb P(A\cap B)=\mathbb P(A)\mathbb P(B\lvert A)\).
| Name | Rule |
|---|---|
| Multiplication rule | \(\mathbb P(A_1\cap A_2\cap\dots A_n)=\mathbb P(A_1)\prod_{i=2}^n\mathbb P(A_i\lvert A_1\cap\dots A_{i-1})\)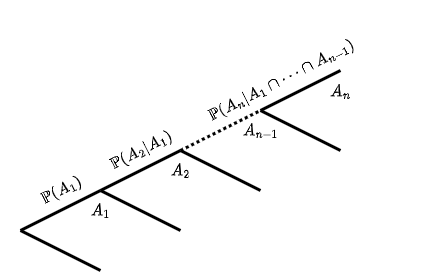 |
| Total probability theorem | \(\mathbb P(B)=\sum_{i=1}^n\mathbb P(A_i)\mathbb P(B\lvert A_i)\) |
| Bayes’ rule | \(\displaystyle\mathbb P(A_i\lvert B)=\frac{\mathbb P(A_i\cap B)}{\mathbb P(B)}=\frac{\mathbb P(A_i)\mathbb P(B\lvert A_i)}{\sum_{i=1}^n\mathbb P(A_i)\mathbb P(B\lvert A_i)}\) |
Bayesian inference, is a three step procedure:
- Draw an initial belief \(\mathbb P(A)\) on possible causes of \(B\)
- Model \(B\) under each \(A_i\), that is \(\mathbb P(B\lvert A_i)\)
- Draw conclusions about causes, \(\mathbb P(A_i\lvert B)\)
When building a model, create a separate branch for every combination events.
Independence
\(A\) is independent from \(B\) when \(\mathbb P(A\lvert B)=\mathbb P(A)\). Accordingly, \(\mathbb P(A\cap B)=\mathbb P(A)\mathbb P(B)\). Often, independence is denoted with \(A\ind B\), is symmetric (\(A\ind B\iff B\ind A\)), allows \(\mathbb P(B)=0\) (as opposed to conditioning), and extends to complements (\(A\ind B\iff A\ind B^C\)).
Conditioning, however, affects independence, and \(\mathbb P(A\cap B\lvert C)=\mathbb P(A\lvert C)\mathbb P(B\lvert C)\) does not mean that \(\mathbb P(A\cap B\lvert C^C)=\mathbb P(A\lvert C^C)\mathbb P(B\lvert C^C)\).
Also, pairwise independence \(\mathbb P(A_i\cap A_j)=\mathbb P(A_i)\mathbb P(A_j), i\neq j\) does not imply collective independence \(\mathbb P(A_1\cap A_2\cap\dots A_n)=\mathbb P(A_2)\mathbb P(A_2)\dots\mathbb P(A_n)\).
Reliability
Reliability is good example of joint probability of independent events. In the table below, \(U\) and \(D\) indicate that the link is up or down, respectively.
| Mode | Diagram | Probability |
|---|---|---|
| Serial |  |
\(\mathbb P(U)=\mathbb P(U_1\cap U_2)=pq\) |
| Parallel |  |
\(\mathbb P(D)=\mathbb P(D_1\cap D_2)=(1-p)(1-q)\) \(\mathbb P(U)=\mathbb P(U_1\cup U_2)=p+q-pq\) (according to inclusion-exclusion formula) |
Assuming \(L_i\in\{0,1\}\) indicates that the network is up when the link \(i\) has failed, then the probability of the network being up despite one element failing is \(\mathbb P(L)=\sum_{i=1}^n \frac{p_i}{\sum_{i=1}^np_i}L_i\).
Go back to the syllabi breakdown.
Back-up
Logical operators
When assessing events, or their combinations, logical operators help expressing in an alternative (and somehow more natural) way set algebra operations. Indeed the following expressions are equivalent.
| description | logical operator | set algebra operator |
|---|---|---|
| \(A\) or \(B\) | \(A\lor B\) | \(A\cup B\) |
| \(A\) and \(B\) | \(A\land B\) | \(A\cap B\) |
| not \(A\) | \(\lnot A\) | \(A^C\) |
| \(A\) implies \(B\) | \(A\implies B\) | \(A\subseteq B\) |
Sum of non negative quantities
Assume you have a collection of \(k\) non negative elements \(\{a_i\}\), s.t. \(a_i\ge0\) for \(i=1,\dots,k\). Let’s define a series of events \(A_i=\left(a_i\lt\frac1k\varepsilon\right)\) and an event \(C=\left(\sum_{i=1}^ka_i\lt\varepsilon\right)\), accordingly in natural language we can say “if every \(a_i\) is smaller than \(\frac1k\varepsilon\), then the sum of \(k\) elements \(a_i\) will be smaller than \(\varepsilon\)”.
\[\begin{align} \bigwedge\limits_{i=1}^k A_i\implies C&&\text{equivalent to}&&\bigcap_{i=1}^k A_i\subseteq C \end{align}\]If we negate (complement) the above expressions we obtain the following statement “if the sum of \(k\) elements \(a_i\) is larger or equal than \(\varepsilon\), then at least one of \(a_i\) is larger or equal than \(\frac1k\varepsilon\)”.
\[\begin{align} \lnot C\implies\bigvee\limits_{i=1}^k\lnot A_i&&\text{equivalent to}&&C^C\subseteq\bigcup_{i=1}^k A_i^C \end{align}\]By computing probabilities of the expression described with set algebra (on the right), we obtain the following relation.
\[\begin{align} \mathbb P(C^C)&\le\mathbb P\left(\bigcup_{i=1}^k A_i^C\right)\\ \mathbb P\left(\sum_{i=1}^k a_i\ge\varepsilon\right)&\le\mathbb P\left(\bigcup_{i=1}^k\left(a_i\ge\frac1k\varepsilon\right)\right)&\text{($A_i\ind A_j$ for every $i\neq j$)}\\ &\le\sum_{i=1}^k\mathbb P\left(a_i\ge\frac1k\varepsilon\right)\\ &=k\mathbb P\left(a_i\ge\frac1k\varepsilon\right) \end{align}\]An alternative result could be obtained starting with the following statement “if the sum of \(a_i\) is bigger than \(\varepsilon\), and one of them is smaller than \(\frac1k\varepsilon\), then the sum of the remaining elements is larger or equal than \(\frac{k-1}k\varepsilon\)”
\[\begin{align} (\lnot C)\land(A_i)\implies&\left(\sum_{j\neq i}a_j\ge\frac{k-1}k\varepsilon\right)&\text{($C\ind A_i$)}\\ \mathbb P\left(\sum_{i=1}^k a_i\ge\varepsilon\right)\mathbb P\left(a_i\lt\frac1k\varepsilon\right)\le\mathbb P&\left(\sum_{j\neq i}a_j\ge\frac{k-1}k\varepsilon\right)\\ \mathbb P\left(\sum_{i=1}^k a_i\ge\varepsilon\right)\left(1-\mathbb P\left(a_i\ge\frac1k\varepsilon\right)\right)\le\mathbb P&\left(\sum_{j\neq i}a_j\ge\frac{k-1}k\varepsilon\right) \end{align}\]